Stochastic Computing

                Ising Solver

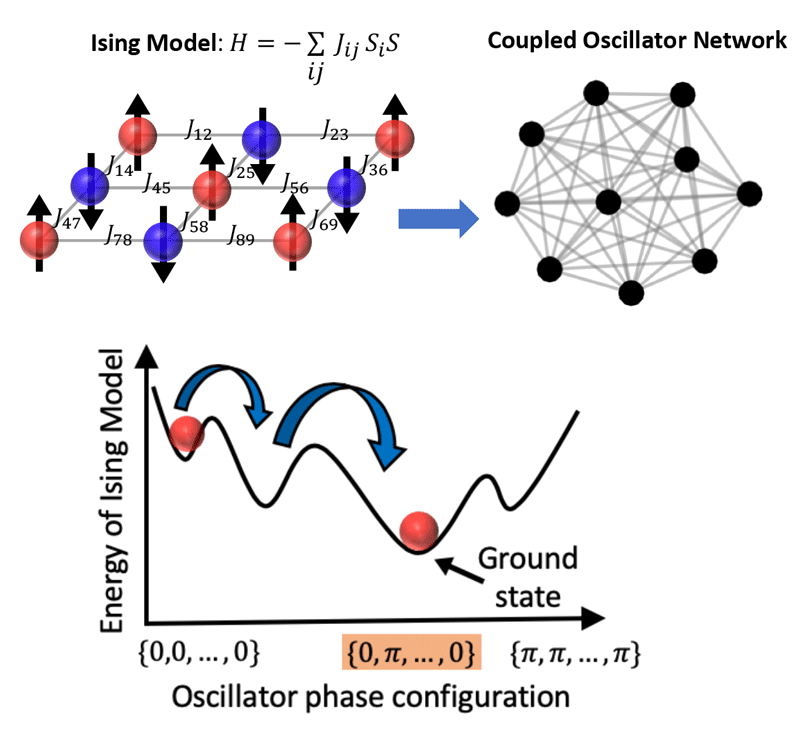
Ising Solver

Ising machines can find the optimal solution to problems involving large number of competing alternatives. This include solving combinatorial optimization problems that are NP-hard. Despite the unprecedented success of digital computing in the last six decades, a class of combinatorial optimization problems still require exponential time or energy to solve them on classical digital machines. Digital computers use simulated annealing or approximate algorithms like semi-definite program (SDP) to solve such problems today. A promising alternative is to map the problem onto the analog continuous time dynamics of a physical system (implementing the Ising Hamiltonian) and take advantage of the inherent convergence property of the system towards an attractor state to obtain the globally optimum solution. We are implemeitng an Ising solver using coupled networks of insulator-to-metal (IMT) phase transition oscillators. We show how resistive and capacitive coupling in such oscillator networks can mimic ferromagnetic and anti-ferromagnetic interaction, respectively, in an equivalent Ising model. We experimentally solve a combinatorial optimization problem – MAX-CUT using IMT oscillator based Ising machine and explore its potential advantages  over other Ising solver implementations from the standpoint of room- temperature operation, programmable coupling scheme, compactness and ease of scalability.

Papers:

1. Dutta, S. et. al. “Experimental Demonstration of Phase Transition Nano-Oscillator Based Ising Machine”, accepted in IEDM 2019

                                      Stochastic Neural Sampling Machine

Stochastic Neural Sampling Machine

Multiplicative stochasticity such as dropout improves the robustness and generalizability of deep neural networks. We are investigating (in collaboration with UC Irvine researchers) the concept of always-on multiplicative stochasticity combined with binary threshold neurons in a novel neural network model called Neural Sampling Machines (NSM). We implement the multiplicative stochasticity using We find that such multiplicative noise imparts a self-normalizing property that implements weight normalization in a natural fashion, and fulfills many of the features of online batch normalization to improve learning rate. Such normalization of neuronal activities during training phase speeds up convergence by preventing internal covariate shift caused by changes in the input distribution.

Papers:

1. Detorakis, G et. al. “Inherent Weight Normalization in Stochastic Neural Networks”, accepted in NeurIPS 2019 

Funded by:

NSF